ちょっと前に娘との円周率の会話が話題になりました。
ポストでは省略していますが、その前に「円周率って無限に続くんだよね。3.14159265358979...。しかも同じ繰り返しがないんだよね」という話があり、その上で「割り切れないんでしょう?」と聞いています。「割り切れない」という言葉は適切ではありませんが、娘は円周率が循環小数でないことを知っているため、これは円周率が無理数であるのはなぜか、という問いになっています。
それについて、僕は小学生に円周率の無理数性を説明しようとして、思わず詰まってしまった、という内容です。
このポストについて、いろいろなコメントが寄せられましたが、僕の意見としては「円周率の無理数性の説明は極限の概念が必要であり、小学生にわかりやすく説明するのは難しい」というものです。
それはそれとして、円周率が無理数であることの説明について誤解があるのかな、と思うレスポンスがあったので、覚書程度にメモを残しておこうと思います。なお、この記事は以下に紹介する説明を非難する意図はありません。「極限操作は直感に反する振る舞いをすることがあるよね」と言いたいだけです。
「円に内接する正N角形を考える。Nを無限大にしないと円にならないので、円周率は無理数である」
この説明で納得している人が多かったように思います。しかし、数列の極限が無理数になるかどうかは別途証明が必要です。また、円周率は直径と円周の長さの比として定義されますが、同様な定義を正多角形に適用すると有理数になりません。
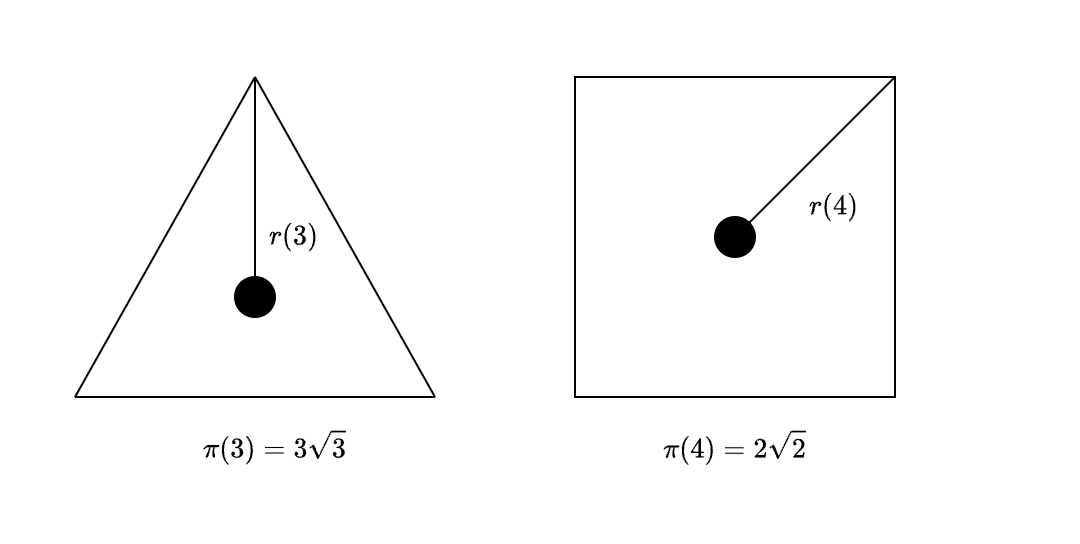
例えば、正N角形の重心を「正多角形の中心」、重心から頂点までの距離を正多角形の【半径】r(N)と定義しましょう。正N角形の周の長さL(N)を、【半径】の2倍で割ったものを、正N角形のN周率π(N)と定義すると、N無限大の極限で円周率になることが期待されます。しかし、例えば正三角形のN周率はπ(3)=3√3、正方形のN周率はπ(4)=2√2となり、どちらも無理数になります。この定義では「周囲の長さを【半径】で割った比」はほとんど無理数です。正六角形は有理数になりますが、他に有理数になるNがあるかは僕にはわかりません。N無限大の極限でこの比が超越数になりますが、有限のNなら必ず代数的数になるかどうかも僕にはわかりません(誰か証明して下さい)。
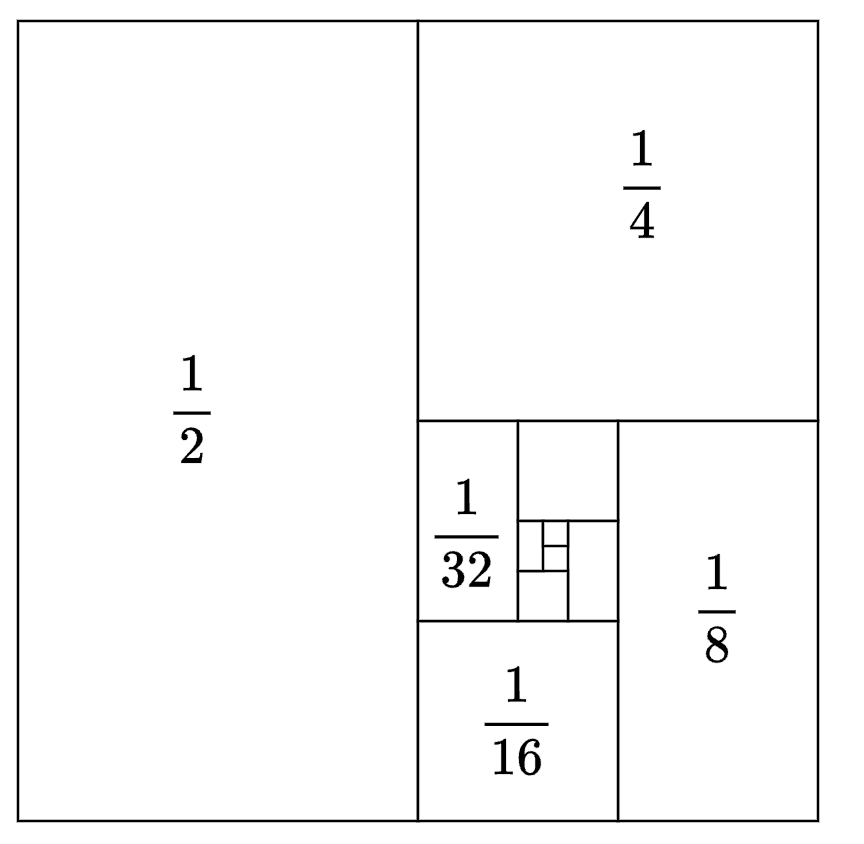
また、「どんどん小さくしていっても必ず隙間が残るから無理数」というロジックも場合によります。よく知られているのは1/2^nの無限和が1となるものです。幾何学的には面積を半分にしながら長方形と正方形を交互に並べていく操作に対応します。この操作をいくら続けても必ず小さい隙間が残りますが、面積の和の極限は1、すなわち有理数になります。
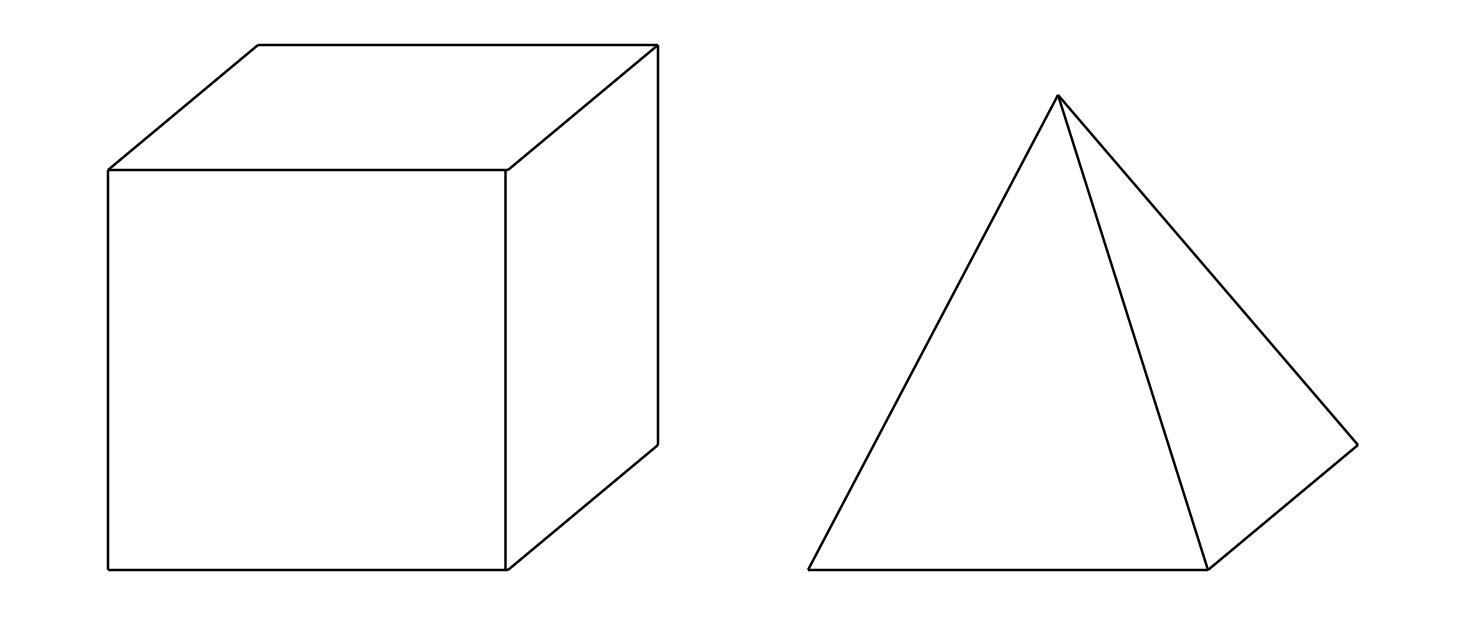
「円の中に小さな正方形をいくら並べても必ず隙間が残るから円周率は無理数」というロジックも適切ではありません。小さい単位図形をうまく並べることができなくても、比が有理数になることがあるからです。例えば、一辺の長さが1であるような立方体と、一辺の長さが1であるような正方形を底面とし、高さが1であるような四角錐の体積比は3:1と有理数になります。しかし、四角錐を小さい立方体で並べ尽くすことはできません。
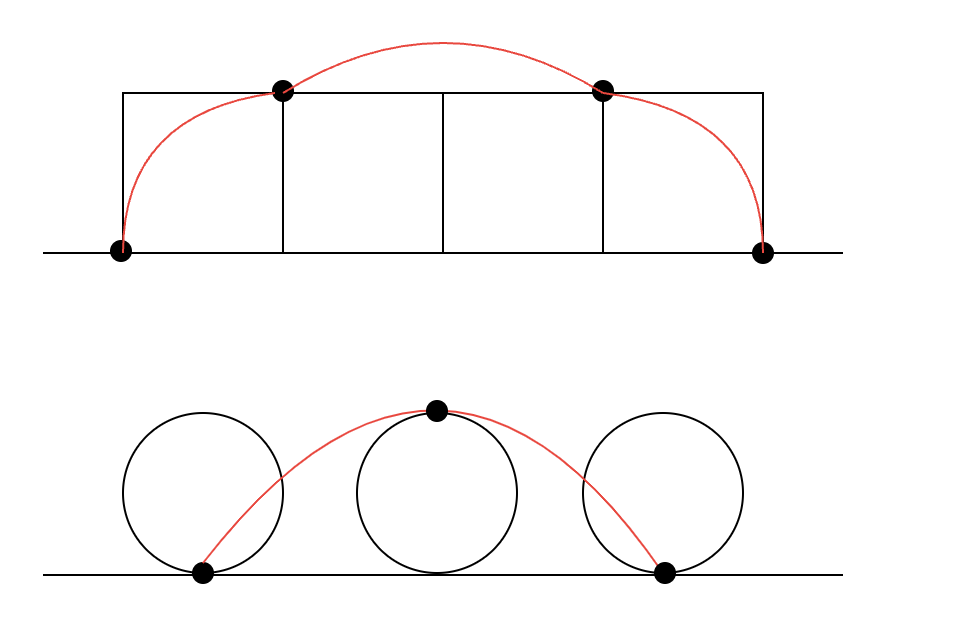
逆に、正N角形では無理数だが、N無限大極限である円なら有理数になるような比を作ることもできます。正多角形を線に接するように一回転させ、その時に頂点がたどる軌跡の長さと、半径との比を考えます。先ほどの【半径】の定義を使うと、正N角形はNが有限である限り、この比は無理数になります(円周率が出てくるので超越数でもあります)。しかし、N無限大の極限である円を回転させたときの点の軌跡はサイクロイド曲線となり、その長さは半径の8倍と、比が有理数になります。
他には、無理数と有理数の濃度比、すなわちランダムに実数を選ぶとalmost surelyに無理数になるから、という説明も見かけましたが、円周率は適当に選んだ数ではないので、これも適切な説明ではないと思います。
いろいろ「あれは駄目だ、これは駄目だ」と書きましたが、じゃあどう説明すれば良かったのかというと、ニーベンの初等的な証明が理解できるツール(微積分、無限和、極限)が揃うのが高校数学からなので、「高校で習う数学を使わないと説明できないから、それまで待ってね」と言うしかなかったかな、と思います。子供向けにわかりやすい説明をすることは大事ですが、それはあくまでも(ある程度)正しくなければいけません。
以上、円周率の無理数性にからめて、つらつら書いてみました。極限操作は直感に反する振る舞いをすることが多いので気をつけなければなりませんが、それ故に面白い話題が多い分野でもあります。