私は数値計算で科学研究を行う、「数値計算屋」と呼ばれる種類の研究者です。数値計算で科学を研究するということはどういうことか、何が面白いのか、簡単に紹介してみようと思います。
数値計算にも多くの種類がありますが、私がやっているのは主にシミュレーションです。シミュレーションとは、興味ある世界をデフォルメして、そのデフォルメされた世界をコンピュータの中で再現し、何が起きるのかを調べる研究手法です。
さて、数値計算屋はデフォルメした世界を創造しますが、手元には、その世界のソースコードがあります。このソースコードを見れば、その小さな世界で起きる全てのことを予想できるでしょうか?
簡単な例をあげましょう。札幌のように、格子状の道を考えます。今、大雪が降ったとして、道が確率1-pで通行止めに、確率pで通行できるとしましょう。このとき、無事な道だけを通って、左端から右端に行ける確率Pは道が無事な確率pについてどのような関数P(p)となるでしょうか?
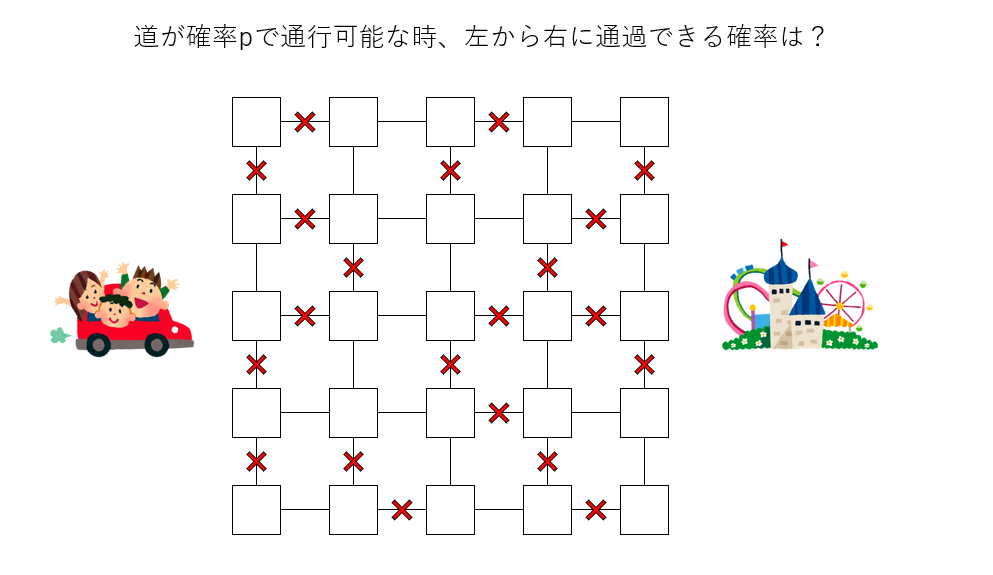
すぐにわかることとして、p=0、つまり全ての道が通行止めなら、絶対に左から右には渡れません。同様に、p=1、つまり全ての道が通行可能なら、必ず左から右に渡れます。したがってP(0)=0, P(1)=1です。ではその間はどうなるでしょうか。
さて、このとても簡単な世界は、とても簡単にプログラムが書けます。あなたがこの世界のプログラムを書くなら、正方格子を準備し、各ボンドを確率1-pで通行不能にして、左辺から右辺まで通行できるかを調べ、その確率Pをpの関数としてプロットすれば良いことになります。その確率Pの振る舞いを、プログラム実行前に予想できるでしょうか?
実は、この世界には、ある臨界確率pcがあり、その値よりもpが少しでも小さいときにはほぼ確実に渡れず、その値よりpが少しでも大きいときにはほぼ確実に渡れる状態になります。
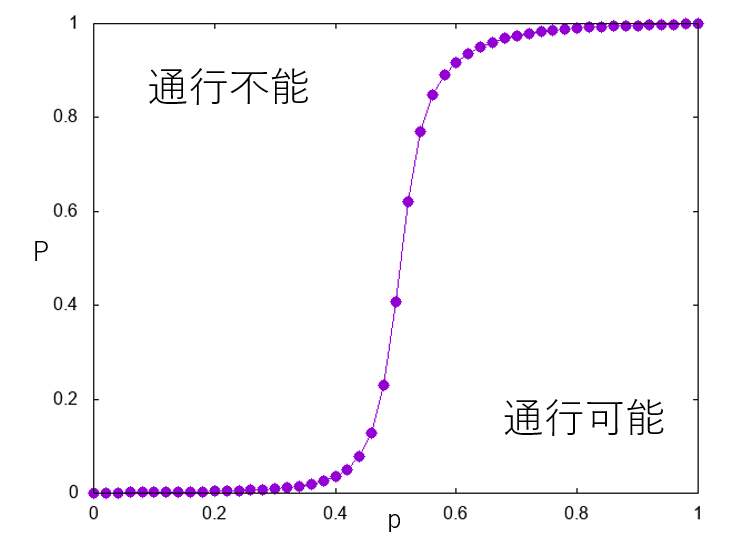
このように、パラメータのある値を境に大きく系の性質が変わることを相転移と呼びます。例えば水は一気圧において、摂氏28度と30度では対して性質が変わりませんが、摂氏99度と101度で全く性質が変わります。これも相転移です。ここで紹介した相転移はパーコレーション転移と呼ばれ、山火事や伝染病をモデル化したものと考えることができます。パラメータpは、火事なら「ある木が燃えたときに、隣の木に延焼する確率」、伝染病なら「ある人が感染した際、隣の人が感染する確率」と考えることができます。先程のP(p)は、何か左端で火事や病気が発生した際、その影響が右端まで届くかどうか、つまり山火事なら山全体が焼けてしまうか、伝染病なら都市全体に感染が広がってしまうかどうかを表しています。先程のグラフは、病気が収束するか拡大するかが、パラメータpに非常に敏感に変化し、p<pcなら収束、p>pcなら拡大と、ガラッと性質が変わるということを主張しています。
なぜ「ある特定のパラメータを境にガラッと変わるのか」をみてみましょう。無事な道路で行き来できる交差点の集まりをクラスタと呼びましょう。クラスタとは「何かの影響が及ぶ範囲」であり、通行確率pが大きくなればなるほど、クラスターは大きくなります。

さて、このクラスタのサイズですが、pを大きくしていくと徐々に大きくなりますが、あるところでクラスタが突然お互いに繋がり、系全体にわたる大きなクラスタが出現します。
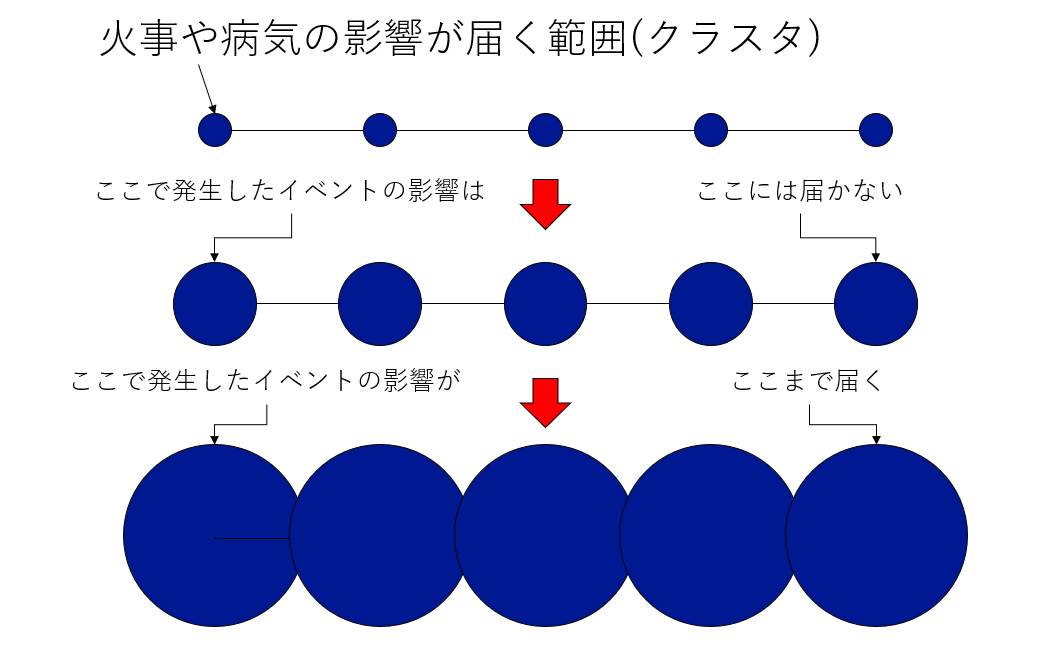
この、クラスタ同士がつながる直前と、つながった直後は、パラメータは少ししか違いませんが、世界の性質は大きく変わります。
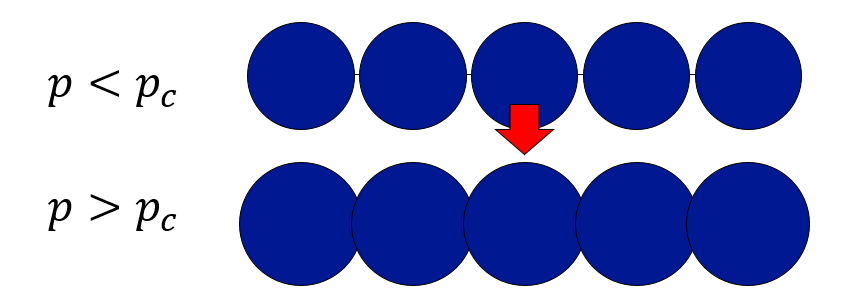
言われてみると、「確かにそうなるかもな」と思うでしょう。しかし、このことを知らずにコードを書いて、実行前に相転移が起きることを予想するのは無理でしょう。
数値計算屋は、このように「デフォルメした世界」をプログラムで表現し、そのプログラムを実行することでデフォルメした世界をシミュレーションし、その仮想世界で何が起きるかを観察することで科学を研究します。自分が創造主であり、世界のソースコードを全て知っているにもかかわらず、何が起きるかわからない、新しい発見が生まれる、それが数値計算の面白さです。
このデフォルメした世界が、ほんとうに現実世界を表現しているのかは難しい問題です。先程のパーコレーションを感染モデルだと思えば、感染確率がある値を超えた瞬間にパンデミックになるため、「いまは大丈夫そうに見えても、ある状態を超えると急に感染拡大するから気をつけよう」と思うことになります。一方で、人が全く動かず、上下左右に人が均等にいて、感染確率が全員同じであるとモデル化するのはあまりに乱暴だと思う人がいるかもしれません。この世界をどこまでデフォルメするか、デフォルメして得られた結果を、どこまで現実世界に適用可能かは非常に難しい問題であり、それも数値計算の面白さの一つです。
この世界が仮想世界であり、自分はAIで、全てがシミュレートされている、と想像したことが一度はあるでしょう。もしこの世界が仮想世界だとすると、世界を作ったプログラマがいるはずです。数値計算屋は、まさにこの立場にいます。神様になって、小さな箱庭に世界を構築し、その世界がどう発展していくかを覗く。数値計算研究とはそういうイメージです。数値計算屋は、自分が創造した世界がどうなるかを予想することができません。そう考えると、もしこの世界全てをプログラムした「創造主」がいたとしても、その「創造主」もまた、この世界がどう発展していくか、全くわからないのではないでしょうか。数値計算をしていると、そんな気がしてきます。