よく議論になるやつ、気になったので調べてみた
帰納法と演繹法
ロジカルシンキングなどで一般的に言われる論理構成(推論法)の中に、帰納法と演繹法がある
どちらも根拠となる情報をもとに結論を導く方法だが、アプローチが異なる
帰納法
いくつかの情報から、一般化された法則や結論を導き出す推論方法
論理構造は以下のようになる
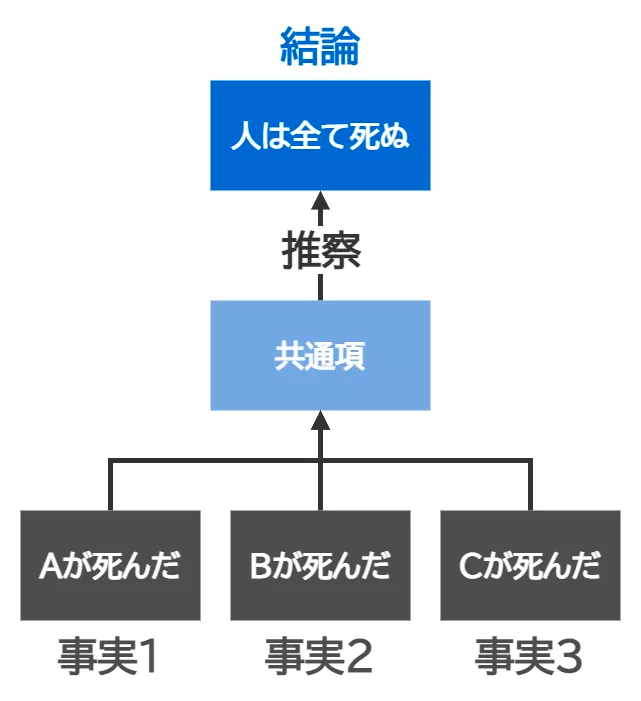
並列する具体事象を一般化して結論を推論するので、論拠となる個別の情報は同次元の情報であることが多い(主語が共通している、述語が共通している、など)
演繹法
一般的な前提から特定の結論を導き出す推論方法
三段論法などと呼ばれることもあり、下記のような論理構造となる
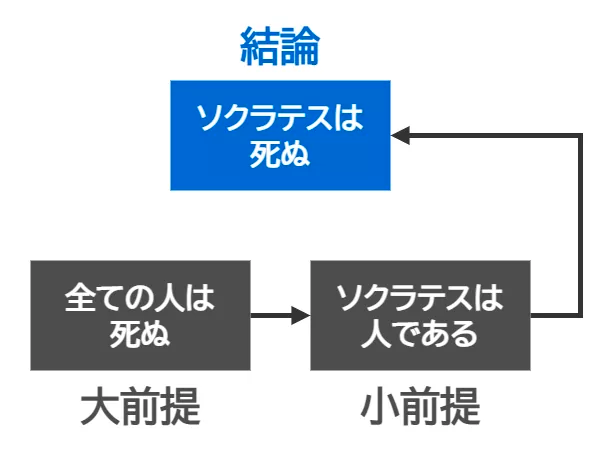
論理の途中で反例が現れることがあるので、段階を踏む際に論理構造の破綻がないか注視する必要がある
数学的帰納法は帰納法か?
数学的帰納法は一般的に以下のプロセスで行われる証明法
自然数 𝑛 に関する命題 𝑃 がすべての自然数 𝑛 について成り立つことを証明したいときに
[基底ステップ]𝑛=1 のとき 𝑃 が成り立つ。
[帰納ステップ]𝑛=𝑘 のとき 𝑃 が成り立つと仮定すると,𝑛=𝑘+1 のときにも 𝑃 が成り立つ。
論理的に、基底ステップが真であれば帰納ステップも必ず真である、という構造になっているので、演繹法的な論理構造に近い(一般化された推論ではなく、基底の情報に反例がある可能性は排除される)
しかし、これは現代的な論理学の分類上はそうなる、という前提がある
日本語訳の問題?
誤訳によって異なる概念に「帰納法」という同じ言葉がついてしまったのか?
というのが気になったので英語でのそれぞれの用語について調べてみる
「数学的帰納法」は "Mathematial induction"
論理推論の帰納法は "Inductive reasoning"、ちなみに演繹法は "Deductive reasoning"
と言うわけで誤訳ではなさそう
ちなみにここにも混同しないようにと記載されているので、この言葉の混同は国際的に発生しているらしい
"Inductive inference" redirects here. Not to be confused with mathematical induction, which is actually a form of deductive rather than inductive reasoning.
数学的帰納法の言葉の由来
探していると、以下の論文で「数学的帰納法」という言葉の語源について研究されているのを見つけた
1600年代、ある自然数𝑛に対する法則を導くのに、𝑛=1, 𝑛=2, ..., 𝑛=6までの例を計算して、𝑛一般について成り立つはずである、という所謂一般的な帰納法に基づく論証が行われたことが起源で、𝑛に対して漸次的に値を代入して論証していく方法を数学的に「Induction(帰納)」と呼ぶようになった、とのことらしい
関係ないけど、ベルヌーイとかド・モルガンとか大物数学者もこの語源に関わってたんだなと思うとなんか面白い
参照
図は以下の記事から拝借