さてさて、前回は尺度について書きました。
データの尺度について考えておくことは、そのデータの特性を理解することにもつながるので、とても大切かと思います。
で、今回はその尺度のなかで最近いろいろ考えている「天井効果」について書き殴っていきたいと思います。
天井効果というのは、その数値の分布が満点(上限)のところに集まってしまうことです。
たとえば今、私たちが小学1年生の算数のテストを受けたとします。
たぶん9割以上の人が満点をとれると思います。
では、高校3年生の数学のテストを受けたらどうでしょうか?
満点をとれる人は少なく、0〜100点の間に分散されるかと思います。
その点数が私たちの算数・数学の実力となりますよね。
でも、小学1年生の算数のテスト結果だけだとどうでしょう?
私たちの9割の人が1位となり、算数・数学の実力は計れなくなります。
これが天井効果ですね。
満点(上限)のところに分布が集まってしまうと、その指標を正しくみれていないかもしれないということです。
逆に0点(下限)のところに集まってしまうことを床効果と言います。
では、BIやFIMだとどうでしょう?
BIやFIMはADLの指標とされており、基本的には順序尺度として取り扱うべき尺度です。
股関節のROMとBIとの関連をみたときに、それらに正の相関があったとします。
股関節の可動域が上がれば上がるほどADLが上がることになります。
そのデータにBIが満点であるデータがいくつかあったらこんな感じになります。
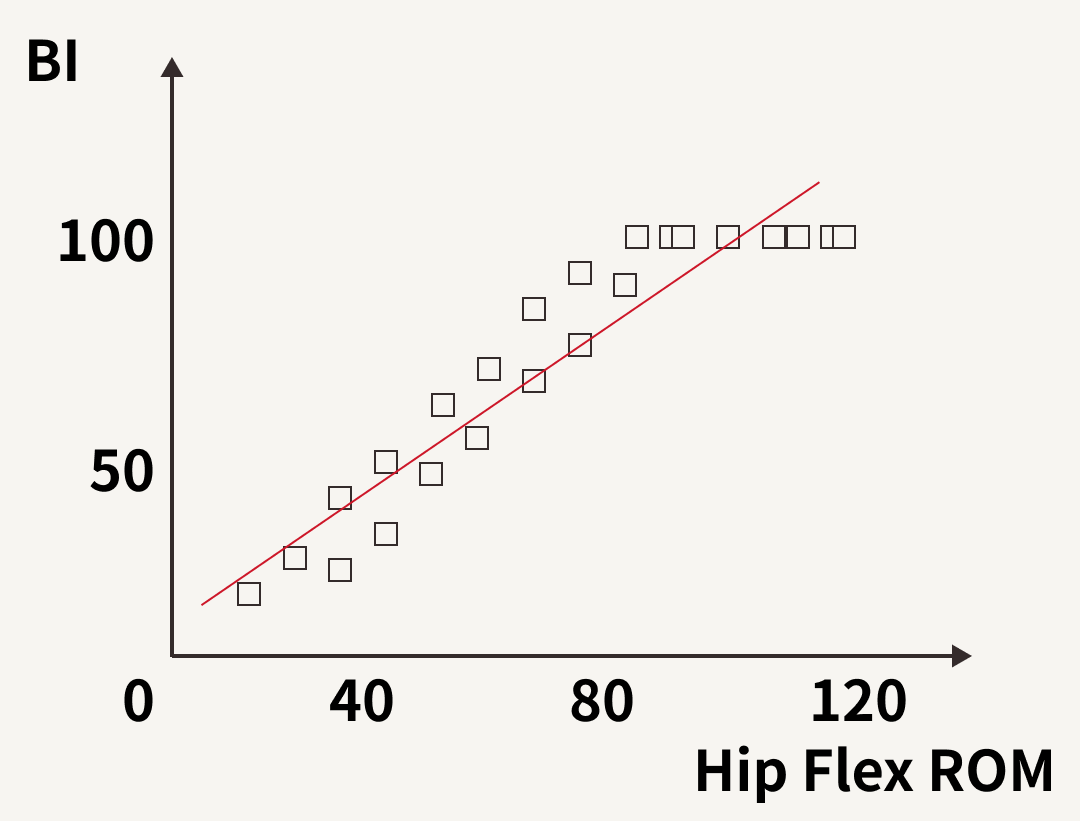
このBIのデータでは天井効果がありますよね?
もし、BIがこの100点の人たちのADLの差も的確に評価できる指標だったらどうでしょう?
BIが150点満点だと100点の人たちの違いもみれそうですよね。
では、150点満点だと…
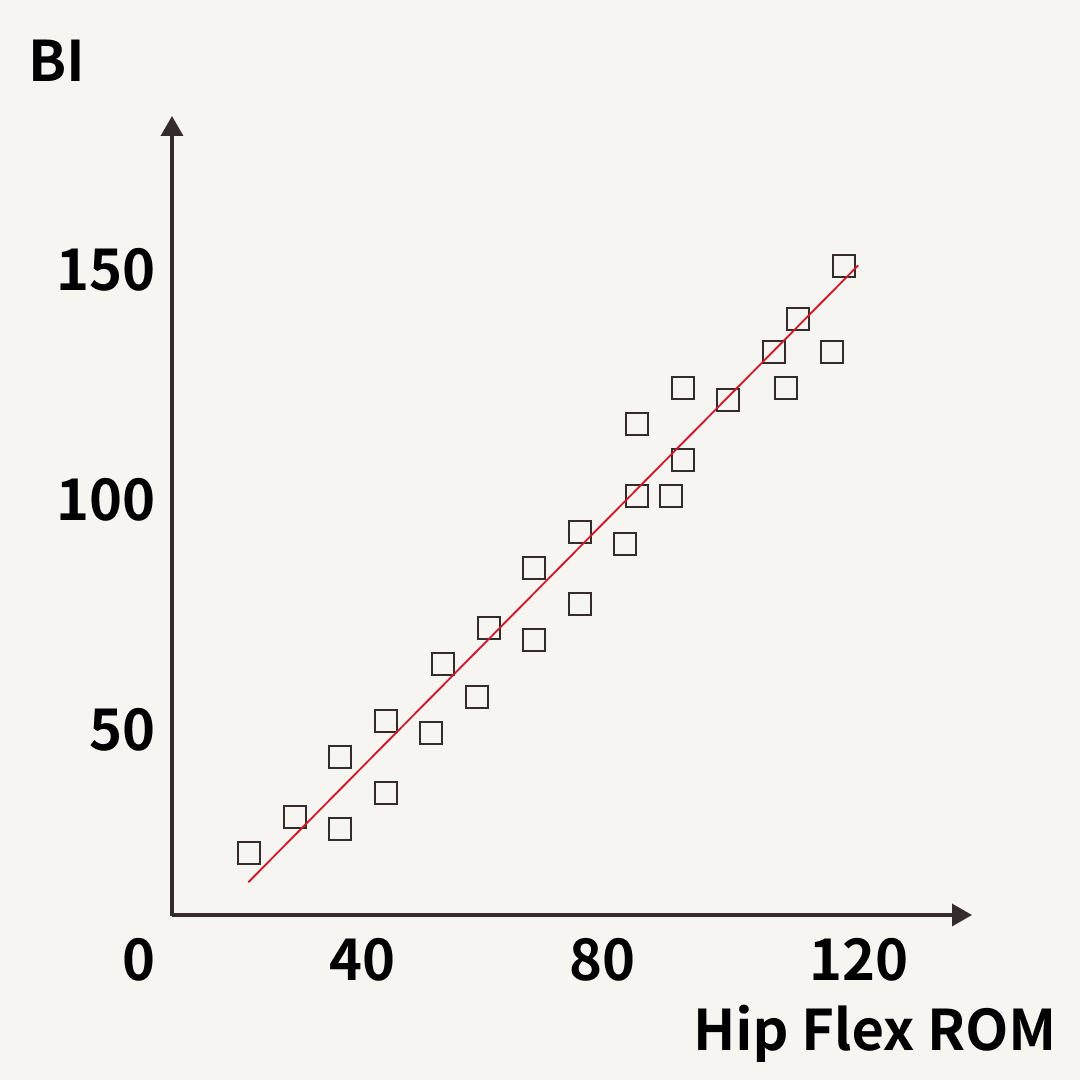
こんな感じですね。
まぁ、恣意的なグラフなのでアレですが、いずれも股関節のROMとBIの間に正の相関関係がみられますが、傾きが変わってますよね?
つまり、天井効果が起こり得るデータにおいてはそこに配慮しないと適切な分析結果が得られないかもしれないということです。
もしかしたら天井効果があったとしても無視しても問題ない場合もあるかもしれません。
たぶんそこはデータ分析についての知識と、その分析したいデータの特性についてのドメイン知識が必要になりそうですね。
あー、むずかしい。
ではではー